-
[NetworkX] 연결중심성, 근접중심성 (Degree Centrality, Closeness Centrality)Data & ML & AI/NetworkX 2022. 12. 7. 00:44반응형
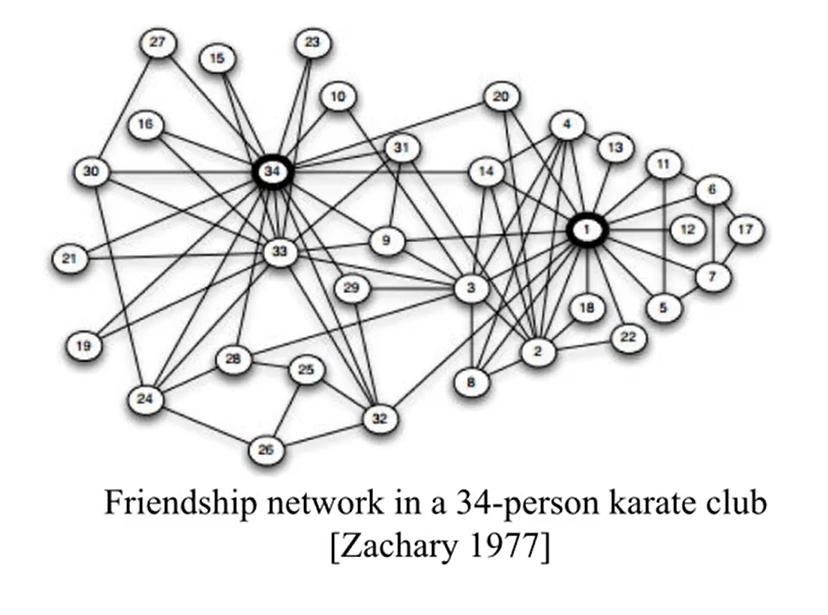
여기에 가라데 클럽에 속한 34명의 친구관계를 나타낸 네트워크 그래프가 있습니다.
import networkx as nx G = nx.karate_club_graph() G = nx.convert_node_labels_to_integers(G,first_label=1)여기서 가장 중요한 노드를 뽑아야 한다면,
무엇이 가장 중요한 노드일까요?
어떤 기준으로 중요한 노드를 뽑을 수 있을까요?
Degree Centrality 연결 중심성
- 아는 친구가 가장 많다면
- = 직접 연결된 관계가 가장 많다면
중요한 노드 아닐까요?
이웃이 얼마나 많은가를 연결중심성(Degree Centrality)이라고 부릅니다.
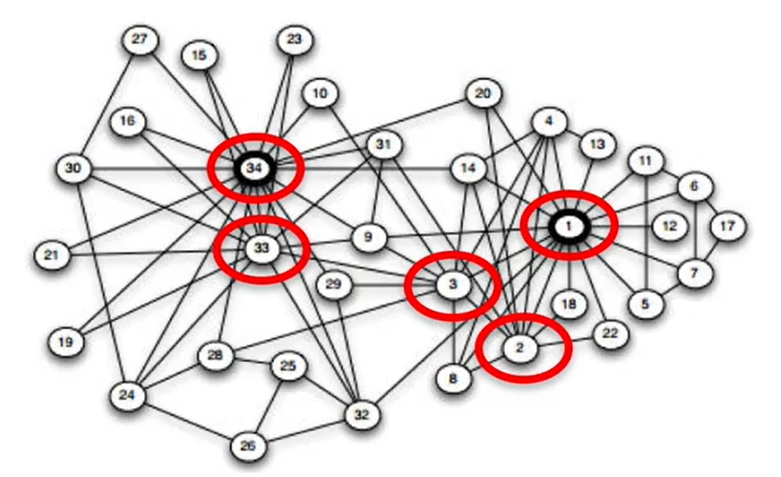
연결 중심성이 높은 노드를 기준으로 중요한 노드를 고른다면,
가장 중요한 노드 5개는 34, 1, 33, 3, 2가 될겁니다.
degCent = nx.degree_centrality(G) # degCent = {1: 0.48484848484848486, 2: 0.2727272727272727, 3: 0.30303030303030304, ... } sorted_nodes = sorted(degCent.items(), key=lambda x:x[1], reverse=True) sorted_nodes[:5] # [(34, 0.5151515151515151), # 17/33 # (1, 0.48484848484848486), # 16/33 # (33, 0.36363636363636365), # 12/33 # (3, 0.30303030303030304), # 10/33 # (2, 0.2727272727272727)] # 9/33방향 그래프에서라면 유입연결중심성(in-degree centrality)과 유출연결중심성(out-degree centrality)를 구할 수 있습니다.
# G = 방향그래프 indegCent = nx.in_degree_centrality(G) outdegCent = nx.out_degree_centrality(G)
각 노드의 연결중심성 공식 - 노드v의 연결중심성 = (v의 degree) / (전체 노드 개수 - 1)
Closeness Centrality 근접 중심성
- 모든 사람들과 몇 다리만 건너도 아는 사이라면
- = 다른 노드들과 근접성이 높다면
- = 다른 노드들과의 최단거리 총 합이 가장 짧다면
중요한 노드가 아닐까요?
다른 노드들과 얼마나 가까운가를 근접중심성(Closeness Centrality)이라고 부릅니다.
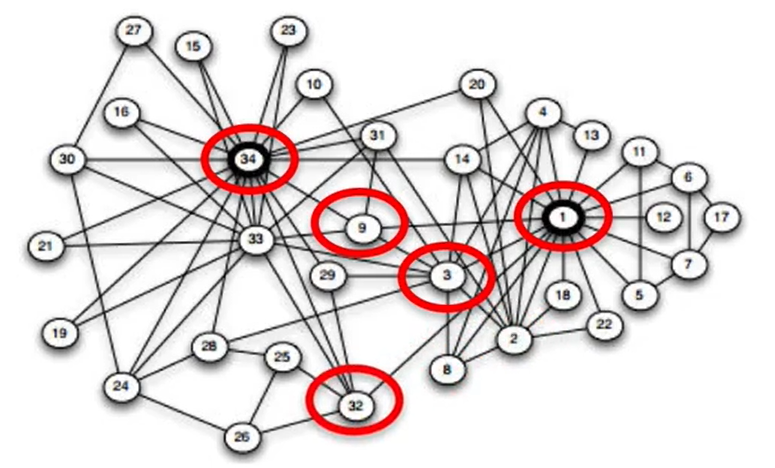
근접 중심성이 높은 노드를 기준으로 중요한 노드를 고른다면,
가장 중요한 노드 5개는 1,3, 34, 32, 9가 될겁니다.
closeCent = nx.closeness_centrality(G) # closeCent = {1: 0.5689655172413793, 2: 0.4852941176470588, 3: 0.559322033898305, ... } sorted_nodes = sorted(closeCent.items(), key=lambda x:x[1], reverse=True) sorted_nodes[:5] # [(1, 0.5689655172413793), # 33/58 # (3, 0.559322033898305), # 33/59 # (34, 0.55), # 33/60 # (32, 0.5409836065573771), # 33/61 # (9, 0.515625)] # 33/64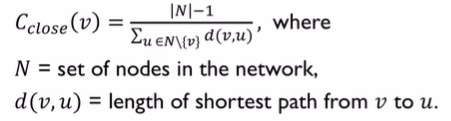
각 노드의 근접중심성 공식 - 노드v의 근접중심성 = (전체 노드 개수 - 1) / 총합(v에서 다른 노드들 까지의 최단거리)
방향그래프에서는 유의해야 하는 점이 있습니다.
도달할 수 있는 노드가 한정되어 있다는 점입니다.
아래의 그래프에서, L이 도달할 수 있는 노드는 M 단 한개 뿐입니다.
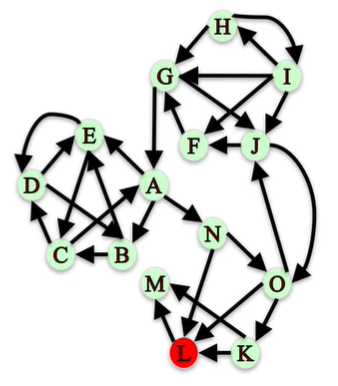
L은 M으로 밖에 갈 수 없습니다. 다른 노드들 까지의 최단거리를 계산할 수가 없습니다. (무한대도 아니고, 0도 아니고, 그냥 불가능하니까요)
이럴 때는 두가지 옵션이 있습니다.
- (1) 도달할 수 있는 노드만 대상으로 closeness centrality를 계산한다.
- (2) 그래프의 전체 노드개수를 고려해 정규화 한 이후 (1)을 계산한다.
# G = 방향그래프 degCent = nx.closeness_centrality(G, normalized=False) # (1)의 경우 norm_degCent = nx.closeness_centrality(G, normalized=True) # (2)의 경우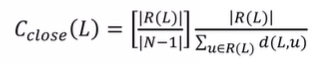
방향그래프에서 각 노드의 근접중심성 공식(2) - (1) 근접중심성(L) = (L이 도달할 수 있는 노드 개수) / 총합(최단거리) = 1/1 =1
- (2) 근접중심성(L) = [(L이 도달할 수 있는 노드 개수) / (전체 노드 개수 - 1)] X (1/1) = (1/14) X 1 = 0.071
본 게시물은 Coursera의 Applied Social Network Analysis in Python(by Daniel Romero)를 통해 자습하며 작성한 게시물입니다.
반응형'Data & ML & AI > NetworkX' 카테고리의 다른 글
페이지랭크 (PageRank) 원리 (0) 2022.12.23 [NetworkX] 매개중심성 (Betweenness Centrality) (0) 2022.12.11 [NetworkX] Assignment 2 - Network Connectivity (0) 2022.11.17 [NetwrokX] 방향그래프의 연결성분(Connected Components) (0) 2022.11.16 [NetwrokX] 그래프 연결성분(연결요소, Connected Components) (0) 2022.11.15